恋愛がうまくいく方法は中学数学がカギ
やっぱり多いんですよ。恋愛で片思いに悩む中学生って。中学生に限ったことでもないですけど。
でもその悩みの種である恋愛も、中学数学の計算を応用するとうまくいく、恋愛成就するなんて言われたら?
よく質問されるんです。「中学数学って勉強しても日常生活で役に立つの?」とか、「三角形の勉強したって日常で使わないじゃん」なんて疑問をいう中学生。疑問というか半ば愚痴。
私も中学生の時そう感じました。「正負の数の計算なんて日常で使わないじゃん」とか、「正の数と負の数を掛け算する時って日常のいつだよ!?」とか・・・。「買い物する時にマイナス500円のおつりって何だよ!? 買い物すれば店が客に金払うのかっ!!」とか本気で思いましたからね。
数学を苦手と感じる生徒は、数学を日常のいつ使うのかという疑問をよく持つように感じます。でもそれって実は素晴らしいことですよね。疑問を持つってことは勉強する姿勢が身についている証拠ですから。だからこそその疑問を持ったセンスを大切に育てていきたいんです。
さぁ、そうするとその疑問に対してどのように答えていくか。
正負の数の掛け算を使いこなせば恋愛が上手くいく
こんなこと言われたら、一瞬興味を持ちますよね?
恋愛は日常生活にありふれたことだし、それと数学が大いに関係しているとしたら、どんな方法なのか知っておきたいと思えますよね。まして片思いで全く進展しない状況にある人にとっては、何とかうまく意中の相手にアプローチする手段を知りたいですよね?
中学1年の時に習った正負の数の掛け算
(+)×(+)=(+)
(+)×(−)=(−)
(+)×(+)×(−)=(−)
などの計算が恋愛に役立つなんてにわかには信じられないですが。
ということでここでは、「数学って勉強して何になるんだよ」とか、「数学を勉強したって意味ないじゃん」など、数学にネガティブな印象を持っている中学生のために、いや、片思いの恋愛などで切実に困っているあなたへ、「恋愛に中学数学、特に正負の数の考え方を当てはめられるよ」っていう理論を1つお伝えします。
この考え方を知っておくと、今まで上手くいかなかった恋愛もちょっとだけ上手く進められるようになるかもしれません。
ハイダーのバランス理論
バランス理論とはハイダーという学者が提唱した説で、「3者間での関係は、それぞれの関係の掛け算の結果が「正」になる時にバランスが取れる」というものです。(ちなみにハイダーのバランス理論は心理学でのお話です。)
ちょっとイメージがつきにくいと思うので次のイラストで考えてください。
ここで正負の数の掛け算の性質を使っていきます。

図のように、「よしこさんとよしお君の関係」「よしこさんとよしひこ君の関係」「よしお君とよしひこ君の関係」は全て円満だったとします。つまり正か負かで言ったら「正」という場合。
この時は「正×正×正」ということで結果「正」となり、バランスが取れていることになります。
みんな仲良くって感じですよね。良いと思います。
では次の場合はどうか?
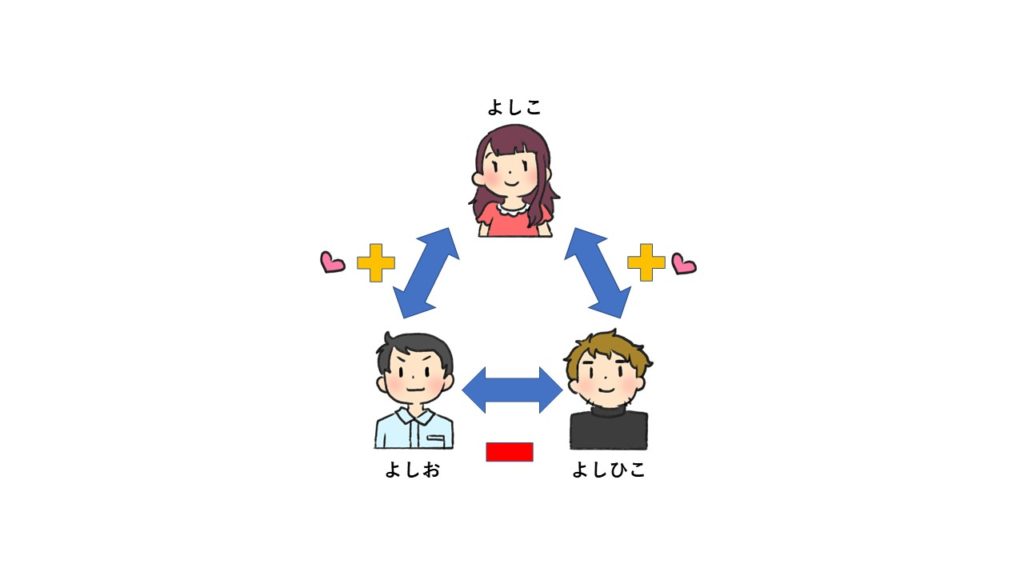
「よしお君とよしこさんは好意を持っている関係」「よしひこ君とよしこさんは好意を持っている関係」「よしお君とよしひこ君はよしこさんを巡るライバルでけんかをしている関係」だったとします。つまりよしお君とよしひこ君の関係が「負」になっている場合。
この時は「正×正×負」ということで結果「負」となり、バランスが取れていないことになります。言い換えれば、頂角をよしこさんとする訳アリの二等辺三角形があり、きな臭さがプンプンの状態だとも言えます。
バランスが取れていない時は普通、バランスが取れるように何らかの変化を起こすものです。日常生活で当てはめると容易に想像つきますよね。
バランスを取るためには何かを変えていかないといけません。
ではどうやってバランスを取るか、つまりどうやって掛け算の結果を「正」にしていくか?
方法として考えられるのは「よしお君とよしひこ君の関係を改善する、つまり正にする」ことですよね。
よしこさんから見たら二人の心をもてあそんで思わせぶりな態度を取っていただけなのかもしれませんが、「けんかを止めて 二人を止めて 私のために争わないで もうこれ以上」っていう感じです。
バランスを取るためには次の方法もあります。
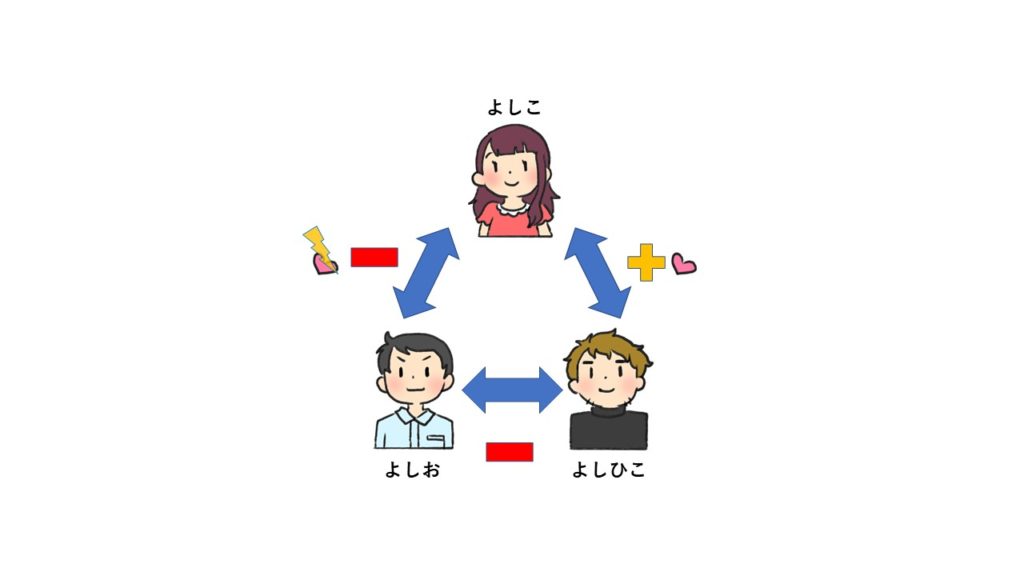
よしお君とよしこさんの関係が「負」になれば「負×負×正」となって、結果「正」となります。よしひこ君からすると願ったり叶ったりの状況です。
よしお君とよしこさんの関係が「負になる」のか、「負にする」のかはわかりませんが、とりあえずバランスは取れるようになります。
さて、あなたならどのようにして3者間の掛け算の結果を「正」にしていきますか?
ハイダーのバランス理論はあくまでも「3者間の関係を単純化した時に当てはまる」ものですからね。現実的には様々なことが複雑に絡み合って関係が成立するから、そうそう簡単に変えていくことは残念ながらできません。ただ、人との関係で何か困ったことがある時にこのバランス理論をちょっと思い出してみると、解決のヒントにはなると思います。
人との関係だけじゃない
上記では人との関係を出しましたが、何も人だけの関係でしか通用しないということではありません。例えば次のように、
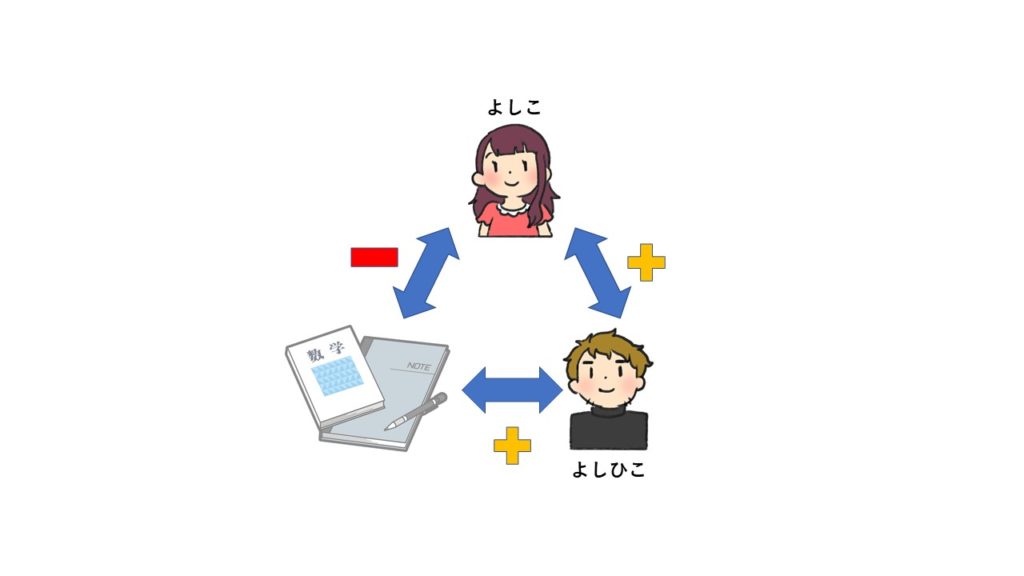
人と物との3者関係でも考えられます。この場合、バランスが取れていません。
何やかんやよしひこ君がうまいことやって、よしこさんとよしひこ君がお近づきになったとします(正)。
よしこさんは数学が嫌いです(負)。
よしひこ君は数学が好きだとします(正)。
よしこさんからしたら、「よしひこは数学と私、どっちが好きなのよ!?」状態です。よしひこ君にとってはたまったものではありません。バランスを取らなければなりません。さあ、どうやってバランスを取るか。
一番簡単な方法はよしひこ君が数学を嫌いになることです。
(+)×(−)×(−)=(+)
でもまぁねぇ、そんなことで数学を嫌いになるとは、よしひこ君の人間性もちょっとあれなんで。
そこでよしひこ君はよしこさんに優しく数学を教えてあげることにしました。そしたらよしこさんは数学が好きになりました。
(+)×(+)×(+)=(+)
結果バランスが取れました。そしてよしこさんとよしひこ君はもっと仲良くなりました。
なんてことだって十分ありますからね。
バランスをとるための別の方法としては、よしひこ君がよしこさんのことを嫌いになるというのもありますが、それではよろしく進めたよしひこ君の行動がムダになります。
恋愛を成就させたいなら三角形を作れ
この記事を読んでくれているあなたは、意中の人がいるものの恋愛が上手くいっていないとします。つまりあなたと意中の人との関係は(−)の状態だとします。この状態の時に意中の人にアプローチしたところで振られるのがオチ。だから一工夫する必要があります。
そこで三角形を作りだしバランス理論を応用していくのです。つまりあなた、意中の人、何かしらの物(人)を頂点とする三角形を想定するのです。
例えばケーキを頂点として用意したとします。
もし意中の人がケーキ嫌いだったら、意中の人とケーキの関係は(−)ですよね。そしたらあなたは、実際はケーキが好きかもしれませんが意中の人の前ではケーキ嫌いを装うのです。
すると、(−)×(−)×(−)=(−)の関係ができてバランスの取れない三角形ができます。これを使うんです。
バランスが取れていない状態をバランスの取れた状態に変えていくのです。
どうするのかって?
意中の人をケーキ好き(+)にしたってしょうがないでしょ。
ケーキをダシにして、あなたと意中の人の関係を(+)に変えていくんです。
(+)×(−)×(−)=(+)
の三角形を作っていくんです。
「ケーキってカロリー高いから太るよね」とか何とかもっともらしいことを適当に言って、あなたとケーキの関係が(−)であることをアピールします(本当はものすげぇ~ケーキ好きだったとしても)。
するとあなたと意中の人の間に、ケーキが嫌いという共通のネタができますよね。この共通のネタがあなたと意中の人の関係を(+)へと変えていくのです。
これでとりあえずあなたと意中の人とは(+)になり、バランスの取れた三角形ができます。でもそれで終わらせるのはもったいない。
本当はあなたはケーキが好きなんです。だから意中の人にもケーキ好きになってもらって一緒にケーキ屋さんに行きたいんです。
そこで意中の人にカミングアウトするのです。「ハチミツって甘い割にカロリー低いんだって。ハチミツを使った甘さ控えめのケーキがあるみたいなんだけどどんなものか食べに行こうよ」みたいな感じで。あなたとケーキの関係が(+)であることを暗に匂わせるのです。
ポイントは一度できたバランスの取れた三角形をあえて崩すこと。
つまり (+)×(+)× (−) = (−) の形をあえて作り出す。
すると・・・、わかりますよねぇ、バランスが取れていない状態ではバランスを取れるように変わっていきたくなるものです。
ここで意中の人をケーキ好きに変えていくんです(+)。
そうすると(+)×(+)×(+)=(+)ができますよね。つまりバランスの取れた三角形が再びできたわけです。
で、ここで終わらせますか?
もっと発展させたいですよね。
ではどうするか?
また新たに物なり人なりを用意してバランスの取れない状態を作り出すのです。そしてそこからバランスの取れた状態にしていく。
以後これの繰り返し。
まとめとして
私が中学生当時、先生に疑問をストレートにぶつけたんですね。「数学を日常生活で使うのはいつなのか」を。
先生は親切に説明してくれるんですよ。数学に少しでも興味関心を持たせようと、私に色々な具体例を示してくれたんです。例えば「ミツバチは図形のエキスパートなんだよ」とか、「ひまわりの種の付き方って数学の本質を突いた美しい並びなんだよ」とか。
話としては面白いんです。確かにへぇ〜とは思うんです。多少は関心も出るには出るんです。ただ、日常という意味ではやっぱりズレを感じていたんですね。クマさんみたいに常にハチミツを探し歩いているわけじゃないし、ひまわりの種の付き方を知ったってハムスターじゃないから別に嬉しくないんです。私としてはもっと直接的に日常生活のどのようなところで役立つのか、勉強した意味を感じられるのか、そういった具体例みたいなことを知りたかったんです。
でおそらく、「数学が日常のいつ役立つのかという疑問を持っている今現在中学生の生徒」も、やはり私と同じようにもっと直接的に日常のいつ役立つのかを知りたいと思っているはずなんです。
随分と下世話なネタで書きましたが、でも決して「数学の考え方自体は非日常のものではない」ということは想像できたかと思います。「人との関係やつながりは掛け算で考えられる」と知れば、数学をまた違った角度から理解できると思います。「優しい言葉をかける」なんて言い方をしますが、心の中では言葉を掛け算して関係を作っているのかもしれませんね。
ここでは計算を対人関係に当てはめた考えを紹介しましたが、図形を対人関係に当てはめた考えもあります。
今回の記事を読んだからといって恋愛が必ず上手くいくというわけではないですが、数学を考える際の別の視点を身につけてくれればいいかなと思っています。そして数学嫌いを少しでも改善、克服につながればうれしい限りです。
中学生にとって興味関心の高い恋愛について数学と絡めてお話することはまだありますので、気が向いたときにまたこんな感じのネタで記事にしてみます。